Kosaraju Algorithm

過程

建立反圖 G^T，在 G^T 上 DFS 並記錄每個點離開的時間

依照離開時間大到小的順序在原圖 G 上 DFS 即可正確找出 SCC

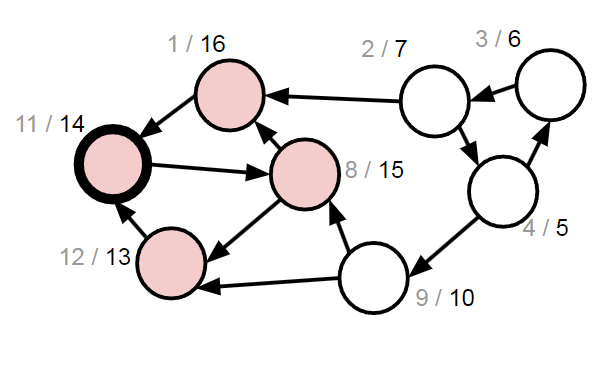
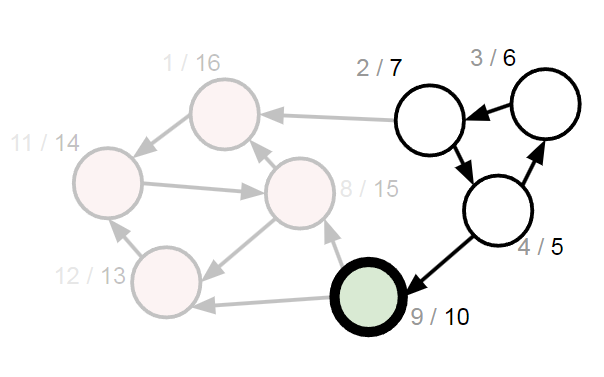
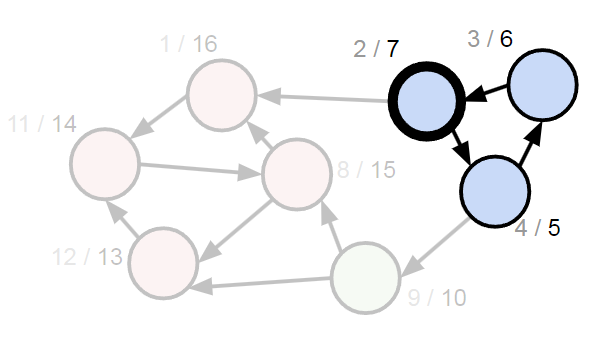
證明

感性理解

若 A 可以走到 B，代表 B 裡面的所有點都要走完才會返回到 A

From 資訊之芽

• 可以用 DAG 的例子來想像 Kosaraju 在做的事

• dfs 一遍照離開順序由大到小 $⟹$$\implies$ 拓撲順序

• 離開順序最大的點 $⟹$$\implies$ 入度 0 的點

• 反圖後這個點就變成出度 0 的點了，他走不到任何人，所以也就當成只會單純蒐集這一個點成一個強連通元件

• 所以我們只是在一直把反圖上出度 0 的點依序移除，你可以當成每個點其實就是一個強連通元件縮成一個點的樣子

From IONC

假設 $G$$G$ 在 DFS 時，節點 $y$$y$ 比節點 $x$$x$ 先進入堆疊，那麼 $G^T$$G^T$ 上 DFS 時會先由節點 $x$$x$ 開始

【Case 1】若在 $G^T$$G^T$ 上 DFS 時，可以由 $x$$x$ 到達 $y$$y$，則代表 $G$$G$ 上存在 $\text{path}(y,x)$$\text{path}(y,x)$

若 $G$$G$ 上不存在 $\text{path}(y,x)$$\text{path}(y,x)$，則一開始在 $G$$G$ 上的 postorder traversal 中結點 $y$$y$ 必須比節點 $x$$x$ 晚進入堆疊，違反假設，因此在這樣的狀況下 $G$$G$ 上必存在 $\text{path}(y,x)$$\text{path}(y,x)$，也就是說 $x$$x$ 和 $y$$y$ 存在同一個強連通分量中。

【Case 2】若在 $G^T$$G^T$ 上 DFS 時，無法由 $x$$x$ 到達 $y$$y$，則代表在 $G$$G$ 上不存在 $\text{path}(y,x)$$\text{path}(y,x)$，$x$$x$ 和 $y$$y$ 都不會存在於同一個強連通分量中，也不會影響到演算法的正確性。

歸納所有 Case 1 的狀況，就能求出所有的強連通分輛，Case 2 則構成了完成縮點後的邊。最後這個證明還缺了一部分 : 這個演算法找出的強連通分量是最大的，此部分留給讀者思考。